PBL Symposium 11 - 12 Jun 09 (Part 8): A simulated PBL lesson

[From Part 7]

On Day-2. 11 June 09.

"What happens if, in a student-led discussion, the entire group goes off track and doesn't grasp basic concepts that they are required to have?"

I asked my friend Mr. Grain Baysa-Pee at lunch today. He's a lecturer Senior Academic Staff at Republic Polytechnic (RP).

He clarified that by the time students make their third and final group presentations for the day's PBL lesson, they would have realised what they don't know, based on what the other groups have presented. Or through probing questions by the facilitator.

"Why can't the facilitator just tell them the concepts?" I queried further.

No, the facilitator should NOT say "That's wrong". The PBL approach was designed to let students internalise the error themselves.

My friend added: "What would (the facilitator) have achieved by telling students the 'right' concepts? It would only have satisfied the facilitator's need to tell them. But students would not know the significance".

I had a chance to internalise what my friend meant, next.

A SIMULATION: PBL in Engineering Education.


The symposium offered a few PBL 'mock' sessions. I attended the engineering-related one.

I've absolutely no engineering background. And I tend to be slow in grasping mathematical concepts (unless I can draw/ visualise it). But the aim of the shortened simulated PBL lesson (RP's unique "One Day One Problem" approach) was not to make an engineer out of me.

In fact, I wanted to experience first hand what a slower student* might feel in a PBL setting.


A 'SIMPLIFIED' PROBLEM
The normal PBL lesson, RP style, spans one full day. There would be a 'First Meeting' and 'First Study Period' (both one hour each). Then a Second Meeting/ Study Period (another hour each). Finally a Third Meeting (two hours).

The First Meeting was to define and understand the problem. The document detailing the 'problem scenario' was preloaded on the laptop:


The stated 'problem' involved percentages and ratios in sourcing and mixing iron-ores to produce steel. Three different country sources meant different costs. The alloy mixtures were sub-categorised by three different grades of steel (A to C), depending on variations to the percentages.


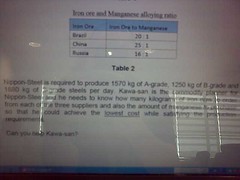
The phrasing of the problem, including the facts stated as part of the problem scenario, were realistic.

The line "Can you help Kawa-san" seems to reinforce the realism.


I re-read the 'problem' three times and still didn't quite get it. This was supposed to be simplified!

Upon hindsight, I think that might have been deliberate. In real-life, we may recognise a 'problem situation' but even so, things may not be clearly defined and require time to clarify.

[ASIDE: KEY ELEMENTS IN RP's PBL]
One of the facilitator, Hisham, explained that the key elements were:

1. Learning environment (group work; 5 students per team; wireless Internet access to allow them to obtain resources, references)
2. Problem statement and Daily Activities (Prob scenario design, 'Scaffolding', Facilitation, Presentation, Assessment)
3. Reflection (student journal)

The problem scenario would be something students can relate to in their daily/ real life. At this point of the PBL session, students are not told of learning objectives. That would only be revealed at the end of the session.

STUCK ALREADY?!
At that point, I felt unsure of what to do next. I couldn't quite appreciate what the guy I was supposed to help, Kawa-san, had to do.

In a hazy way, I knew he had to make a decision on how much iron ore to buy from each source. But I wasn't quite clear how to approach it.

Then the facilitator introduced a "problem definition template". It was a simple three-column table with the headers: "What do you already know, based on prior knowledge"; "What don't you know or are unsure"; "What do you need to find out?"


PROBLEM DEFINITION TEMPLATE
A quick discussion with my team partner (there were only two of us in the group) resulted in this:


At the second column, "What I do not know" , I wrote point 2: "What (does) the ratio for (mixing the) alloy mean". I wrote that with some reluctance, as I shall explain further.

Each team had to explain their problem definition template. Facilitators would ask probing questions at this point. My team was asked to clarify what we wrote for "Don't Know/ Unsure". Particularly point 2.

So I honestly said, "The facts are just data to me. There is no meaning as I look at the stated numbers and ratios".


OVERCOMING THE FEAR OF REVEALING ONE'S IGNORANCE
In a classroom setting, it was quite daunting to admit in front of strangers that you don't know something!

It didn't help when one other group was very advanced and already in the process of devising a mathematical solution to the problem. They had superior prior knowledge (not surprising, as they comprised of participants who were probably engineers with PhDs).

Yet I was glad I went for honesty instead of feigning intelligence.

Because after I explained to the class that the ratios don't hold meaning to me, the facilitator asked the 'advanced' group how they understood the ratio.

That group paused and stared. They hesitated.

It was as if I'd asked an extremely rudimentary question. Too simple to have even been raised at all, at this level.

But it turned out that group had made certain assumptions. As well as others.

The advanced group said, "We'd assumed it meant 'weight'".

"Ah, the unit of measurement isn't stated in the problem," prompted the facilitator. Whereby another group quickly said they'd assumed it meant "mass".

Suddenly I didn't feel that stupid for raising the question!


QUESTIONING ASSUMPTIONS
The facilitator deftly focused the discussion on whether the ratio meant "weight" or "volume" or "mass". Finally there was consensus on interpreting what the ratio meant.

I kept quiet throughout that episode. But my mind was actively making sense of the discussion. The ratios meant something to me now. Pretty simple yet amazing process, I thought.

For me, that simple act of admitting my ignorance, and the facilitators being able to channel that as a discussion point, clarified what I was really not able to articulate when I wrote "I don't know".

The simple three-column "problem definition template" allowed for interpretations and assumptions to surface. This was something I can bring back and share with colleagues. When delving into complex problem scenarios, there's a risk of interpreting the problem wrongly. Using the template may help negate that.


SCAFFOLDING
Then a second worksheet was given. There were more questions for us to consider (e.g. how would the problem be formulated from the perspective of 'cost'? Or maximising 'profits'?)

Basically more prompts to help us frame and conceptualise the problem.


This aspect of PBL was termed as a "scaffold". I understood it to mean various supporting tools -- worksheets or computer simulation programs -- anything that helps the student to frame and understand the problem better.



FACILITATE, NOT GIVE ANSWERS
The facilitators do not offer answers or solutions at any stage. They aimed to nudge students towards developing their own solutions.

In the mock PBL, at no point did the facilitators say "look up to solve the problem".

We were guided on writing and expressing the problem statements as equations. Which was a handy want to conceptualise the statements. That itself seems to be a hint but the faciliators stopped short of telling you what to do next.


INTERNALISING THE PROBLEM
I understood better how inherent in PBL was the process to make students internalise the the problem.

Contrast this with traditional teaching, where problems are merely given to students. The aim was to make students arrive at a solution (often a limited one), rather than to appreciate the problem and therefore being able to explore deeper solutions to the problem.

I asked: what if some students developed a solution without using the method/ intended concept to be gained for that session? E.g. instead of using linear programming, what if student develops a complicated but valid way to develop a solution?

"It's OK. It's the process."

It might not be exactly the answer. Or it might take a longer time to derive the answer. But in real world it might still work. That's how I understood it.

I also realised the logic to the above approach is that a student would realise which solution was the more elegant and efficient one. Which means greater understanding and appreciation of the 'preferred solution'.


HOW WOULD ALL STUDENTS LEARN WHAT THEY HAVE TO LEARN?
At that point I asked a facilitator how they would ensure all students picked up the same learning objectives?

For instance, what was the lesson of the day? Something to do with Simultaneous Equations? Or what?

Since this was a mock tutorial, I was told the lesson objective was about Linear Programming.

The facilitator explained that through group presentations, students would have to explain the rationale for their solution. Like why they decided on certain approaches; use of certain principles or concepts. Through open-ended questions, they are further prompted to explain the process of arriving at the group decisions.

Through this process, required concepts would be uncovered. If solutions presented were incomplete, other students would help out.

Another way to ensure students get to learn the required concepts is through reading materials distributed at end of the day (rather than at the start).


ASSESSMENT
The assessment module (via their LEO module, mentioned here) was also part of the process to determine if students have identified and understood the required concepts.

Daily grades are the main assess tools. The student presentations would confirm their understanding. There could also be quizzes and other such means of assessment. There are also written tests to check their level of understanding (Understanding Tests).



TEACH LESS, LEARN MORE
As I reflect on the mock PBL session, I'm reminded of our MOE's Teach Less, Learn More doctrine.

Seems to be RP is doing right in this regards.

I'm amazed there's no "instructional teaching/ telling" at all. Students are assessed on their level of engagement, their participation. Those who don't meet the expected level of participation would ultimate get a Fail grade for the day.

In an actual RP's PBL session, students would not be told they were learning about Linear Programming (which was what the simulation was about).

That seems to be the old way, where topics are stated at the start. I think the logic is that when you state the learning objectives immediately, there's a tendency to focus on the outcomes rather than the process.



***

Thanks to the RP academic staff for ably leading the simulated session: Urvi Maniar, Tan Yee Ping, Lim Chiew Yen and Hisham Moosa

(Twitter hashtag #pbl09w)

[Next: Part 9]